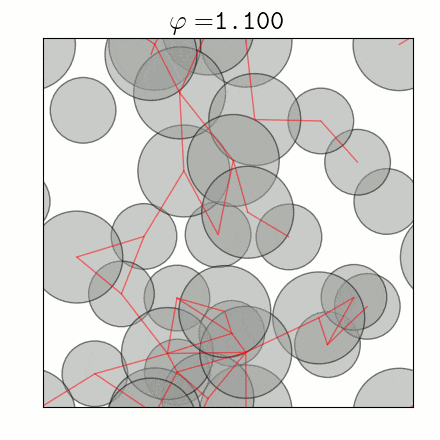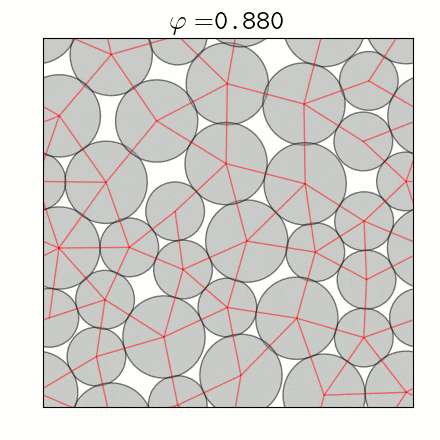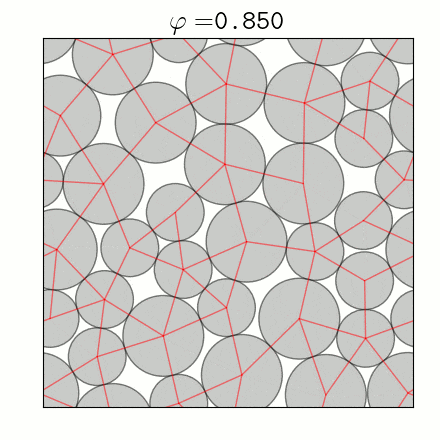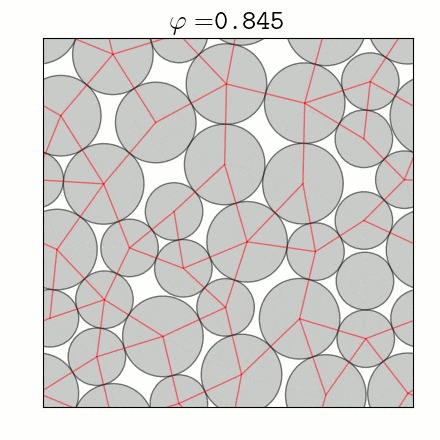
Traditionally, high strength lightweight materials are created from mechanically rigid structures with a combination of compressive and tensile forces. By contrast, purely compressive materials such as sand and gravel do not typically offer a high strength to weight ratio. By considering sphere packings in which all forces are compressive, we determine the limits on creating low density rigid systems. An Apollonian sphere packing proves that a rigid packing can completely fill space, but what is the lowest density a stable packing can achieve?
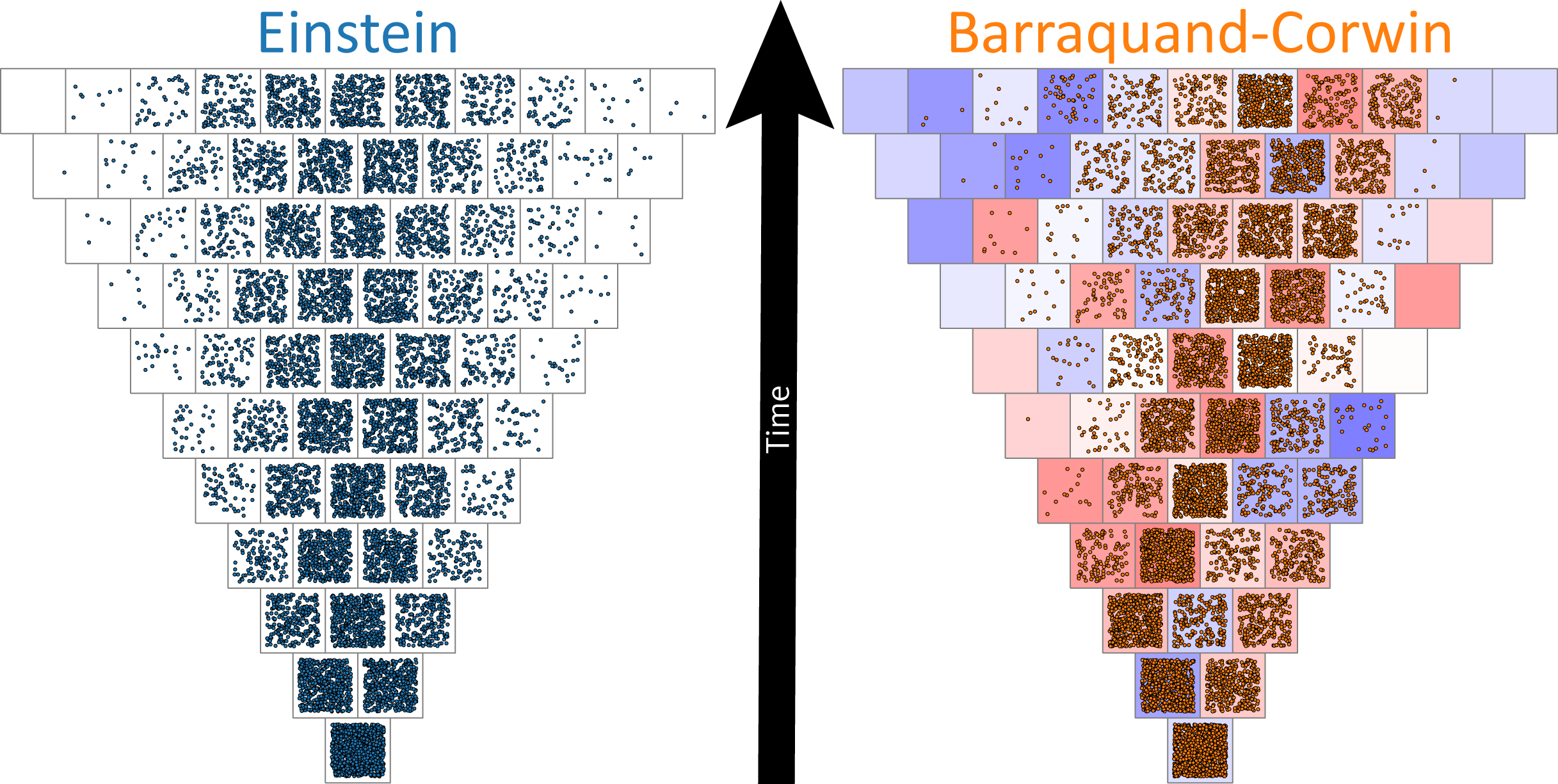
Diffusion is pervasive in the natural world. Over one hundred years ago Einstein created a remarkably simple and effective theory describing the behavior of a single diffusing particle that has since been applied countless times to widely disparate physical systems. We will show that for large numbers of particles diffusing in the same environment, this theory does not correspond to reality as it neglects the effects of the common environment in which all particles live.
In critical phenomena, quantities generally obey power law relations from a critical point. In jamming, the exponents to the power laws between pressure, packing fraction, and number of excess contacts can be derived exactly in the limit of infinite dimensions by the mean field theory of glasses and jamming. While these exponents are expected to be exact above the upper critical dimension, the prefactors to these power law scalings are generally not.
Are all contacts in a granular material created equal? We examine how contacts between particles in granular materials are made and broken by measuring how the force networks in a packing respond to changes in density. We examine the theoretically allowed space of force networks by calculating them as the force network ensemble, and by measuring the size of this space we have successfully characterized the entropy contribution of the force networks.
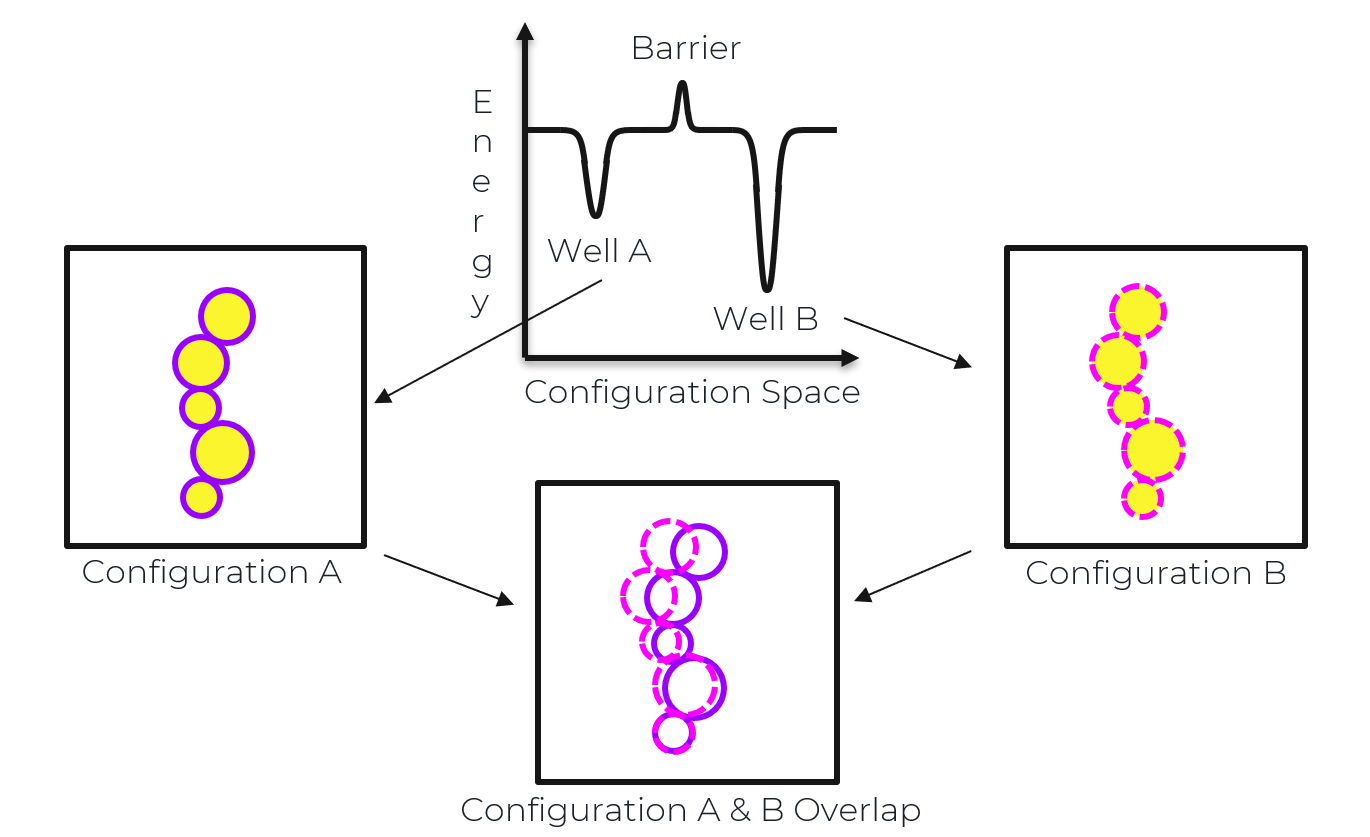
By using random perturbations, the uniform exploration of the jamming energy landscape of simulated, athermal glass particle systems in 3 dimensions can be used to determine all possible minima. Mean-field theory predicts extended configurational changes are responsible for differences between nearby energy wells. In other words, the majority of the system’s glass particles make small, collective motions that lead to differences between neighboring minima. I am interested in understanding if this prediction holds true in 3 dimensions or if differences between minima in low dimensions are controlled by localized movements, in which only a fraction of the system particles move between the associated configurations of neighboring energy wells.
The free energy landscape of mean field marginal glasses is ultrametric. We demonstrate that this feature persists in finite three dimensional systems which are out of equilibrium by finding sets of minima which are nearby in configuration space. By calculating the distance between these nearby minima, we produce a small region of the distance metric. This metric exhibits a clear hierarchical structure and shows the signature of an ultrametric space. That such a hierarchy exists for the jamming energy landscape provides direct evidence for the existence of a marginal phase along the zero temperature jamming line.
When an external deformation is applied to an amorphous solids, its mechanical response is dictated by the degree of stability in terms of its energy landscape. If the system is in a marginal state, tiny perturbations can lead the system to change its state and end up in a different energy minimum, whereas if the system finds itself in a configurations which corresponds to a very deep minimum in the landscape, a much stronger perturbation is required to drive the system away from its state.