Correlations Between Neighboring Minima in Jamming

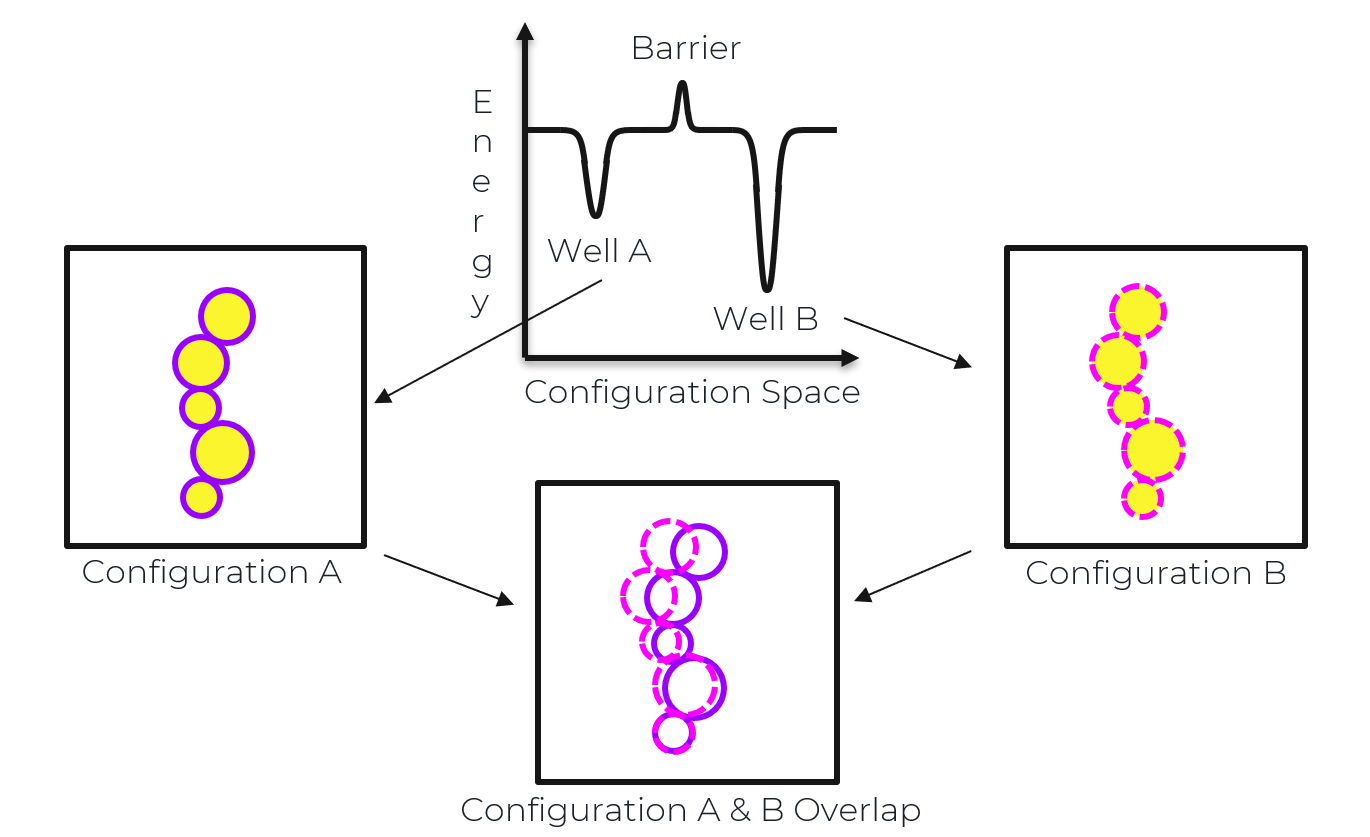
By using random perturbations, the uniform exploration of the jamming energy landscape of simulated, athermal glass particle systems in 3 dimensions can be used to determine all possible minima. Mean-field theory predicts extended configurational changes are responsible for differences between nearby energy wells. In other words, the majority of the system’s glass particles make small, collective motions that lead to differences between neighboring minima. I am interested in understanding if this prediction holds true in 3 dimensions or if differences between minima in low dimensions are controlled by localized movements, in which only a fraction of the system particles move between the associated configurations of neighboring energy wells. Computational results supporting the former may point to the universality of the marginal Gardner phase in amorphous materials.